How to Use Associative Knowledge Graphs to Build Efficient Knowledge Models

In this article, I will present how associative data structures such as ASA-Graphs, Multi-Associative Graph Data Structures, or Associative Neural Graphs can be used to build efficient knowledge models and how such models help rapidly derive insights from data. 

Moving from raw data to knowledge is a difficult and essential challenge in the modern world, overwhelmed by a huge amount of information. Many approaches have been developed so far, including various machine learning techniques, but still, they do not address all the challenges. With the greater complexity of contemporary data models, a big problem of energy consumption and increasing costs has arisen. Additionally, the market expectations regarding model performance and capabilities are continuously growing, which imposes new requirements on them.

These challenges may be addressed with appropriate data structures which efficiently store data in a compressed and interconnected form. Together with dedicated algorithms i.e. associative classification, associative regression, associative clustering, patterns mining, or associative recommendations, they enable building scalable and high-performance solutions that meet the demands of the contemporary Big Data world. 

The article is divided into three sections. The first section concerns knowledge in general and knowledge discovering techniques. The second section shows technical details of selected associative data structures and associative algorithms. The last section explains how associative knowledge models can be applied practically. 

From Data to Wisdom

The human brain can process 11 million bits of information per second. But only about 40 to 50 bits of information per second reach consciousness. Let us consider the complexity of the tasks we solve every second. For example, the ability to recognize another person’s emotions in a particular context (e.g., someone’s past, weather, a relationship with the analyzed person, etc.) is admirable, to say the least. It involves several subtasks, such as facial expression recognition, voice analysis, or semantic and episodic memory association.

The overall process can be simplified into two main components: dividing the problem into simpler subtasks and reducing the amount of information using the existing knowledge. The emotional recognition mentioned earlier may be an excellent specific example of this rule. It is done by reducing a stream of millions of bits per second to a label representing someone’s emotional state. Let us assume that, at least to some extent, it is possible to reconstruct this process in a modern computer. 

This process can be presented in the form of a pyramid. The DIKW pyramid, also known as the DIKW hierarchy, represents the relationships between data (D), information (I), knowledge (K), and wisdom (W). The picture below shows an example of a DIKW pyramid representing data flow from a perspective of a driver or autonomous car who noticed a traffic light turned to red. 

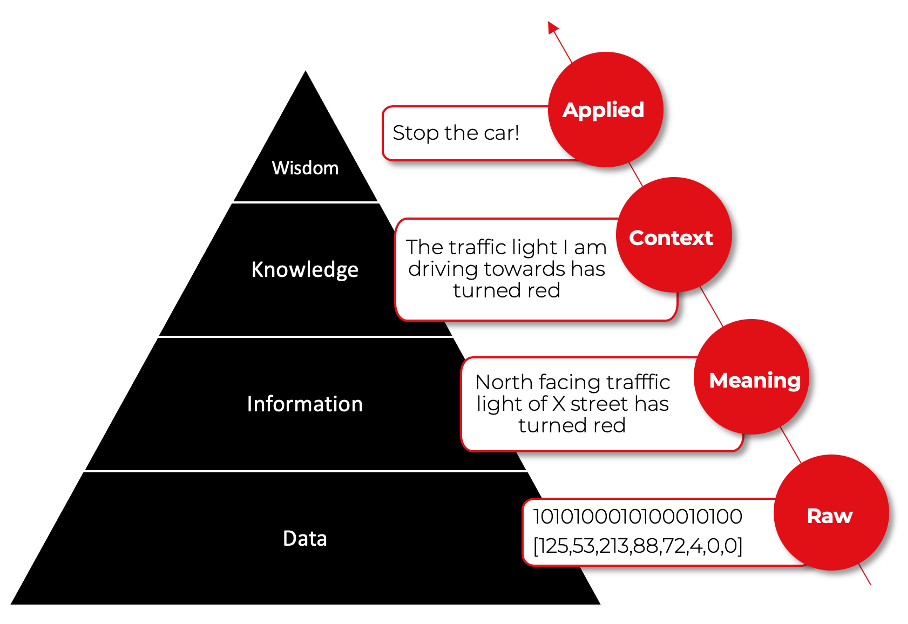
In principle, the pyramid demonstrates how the understanding of the subject emerges hierarchically – each higher step is defined in terms of the lower step and adds value to the prior step. The input layer (data) handles the vast number of stimuli, and the consecutive layers are responsible for filtering, generalizing, associating, and compressing such data to develop an understanding of the problem. Consider how many of the AI (Artificial Intelligence) products you are familiar with are organized hierarchically, allowing them to develop knowledge and wisdom.   

Let’s move through all the stages and explain each of them in simple words. It is worth realizing that many non-complementary definitions of data, information, knowledge, and wisdom exist. In this article, I use the definitions which are helpful from the perspective of making software that runs associative knowledge graphs, so let’s pretend for a moment that life is simpler than it is. 

Data – know nothing

Many approaches try to define and explain data at the lowest level. Though it is very interesting, I won’t elaborate on that because I think one definition is enough to grasp the main idea. Imagine data as facts or observations that are unprocessed and therefore have no meaning or value because of a lack of context and interpretation. In practice, data is represented as signals or symbols produced by sensors. For a human, it can be sensory readings of light, sound, smell, taste, and touch in the form of electric stimuli in the nervous system.

In the case of computers, data may be recorded as sequences of numbers representing measures, words, sounds, or images. Look at the example demonstrating how the red number five on an apricot background can be defined by 45 numbers i.e., a 3-dimensional array of floating-point numbers 3x5x3, where the width is 3, the height is 5, and the third dimension is for RGB color encoding. 

In the case of the example from the picture, the data layer simply stores everything received by the driver or autonomous car without any reasoning about it. 

Information – know what 

Information is defined as data that are endowed with meaning and purpose. In other words, information is inferred from data. Data is being processed and reorganized to have relevance for a specific context – it becomes meaningful to someone or something. We need someone or something holding its own context to interpret raw data. This is the crucial part, the very first stage, where information selection and aggregation start.

How can we now know what data can be cut off, classified as noise, and filtered? It is impossible without an agent that holds an internal state, predefined or evolving. It means considering conditions such as genes, memory, or environment for humans. For software, however, we have more freedom. The context may be a rigid set of rules, for example, Kalman filter for visual data, or something really complicated and “alive” like an associative neural system. 

Going back to the traffic example presented above, the information layer could be responsible for an object detection task and extracting valuable information from the driver’s perspective. The occipital cortex in the human brain or a convolutional neural network (CNN) in a driverless vehicle can deal with this. By the way, CNN architecture is inspired by the occipital cortex structure and function.

Knowledge – know who and when 

The boundaries of knowledge in the DIKW hierarchy are blurred, and many definitions are imprecise, at least for me. For the purpose of the associative knowledge graph, let us assume that knowledge provides a framework for evaluating and incorporating new information by making relationships to enrich existing knowledge. To become a “knower”, an agent’s state must be able to extend in response to incoming data.

In other words, it must be able to adapt to new data because the incoming information may change the way further information would be handled. An associative system at this level must be dynamic to some extent. It does not necessarily have to change the internal rules in response to external stimuli but should be able to at least take them into account in further actions. To sum up, knowledge is a synthesis of multiple sources of information over time. 

At the intersection with traffic lights, the knowledge may be manifested by an experienced driver who can recognize that the traffic light he or she is driving towards has turned red. They know that they are driving the car and that the distance to the traffic light decreases when the car speed is higher than zero. These actions and thoughts require existing relationships between various types of information. For an autonomous car, the explanation could be very similar at this level of abstraction. 

Wisdom – know why

As you may expect, the meaning of wisdom is even more unclear than the meaning of knowledge in the DIKW diagram. People may intuitively feel what wisdom is, but it can be difficult to define it precisely and make it useful. I personally like the short definition stating that wisdom is an evaluated understanding.

The definition may seem to be metaphysical, but it doesn’t have to be. If we assume understanding as a solid knowledge about a given aspect of reality that comes from the past, then evaluated may mean a checked, self-improved way of doing things the best way in the future. There is no magic here; imagine a software system that measures the outcome of its predictions or actions and imposes on itself some algorithms that mutate its internal state to improve that measure. 

Going back to our example, the wisdom level may be manifested by the ability of a driver or an autonomous car to travel from point A to point B safely. This couldn’t be done without a sufficient level of self-awareness. 

Associative Knowledge Graphs

Omnis ars nature imitatio est. Many excellent biologically inspired algorithms and data structures have been developed in computer science. Associative Graph Data Structures and Associative Algorithms are also the fruits of this fascinating and still surprising approach. This is because the human brain can be decently modeled using graphs. 

Graphs are an especially important concept in machine learning. A feed-forward neural network is usually a directed acyclic graph (DAG). A recurrent neural network (RNN) is a cyclic graph. A decision tree is a DAG. K-nearest neighbor classifier or k-means clustering algorithm can be very effectively implemented using graphs. Graph neural network was in the top 4 machine learning-related keywords 2022 in submitted research papers at ICLR 2022 (source).  

For each level of the DIKW pyramid, the associative approach offers appropriate associative data structures and related algorithms.  

At the data level, specific graphs called sensory fields were developed. They fetch raw signals from the environment and store them in the appropriate form of sensory neurons. The sensory neurons connect to the other neurons representing frequent patterns that form more and more abstract layers of the graph that will be discussed later in this article. The figure below demonstrates how the sensory fields may connect with the other graph structures.  

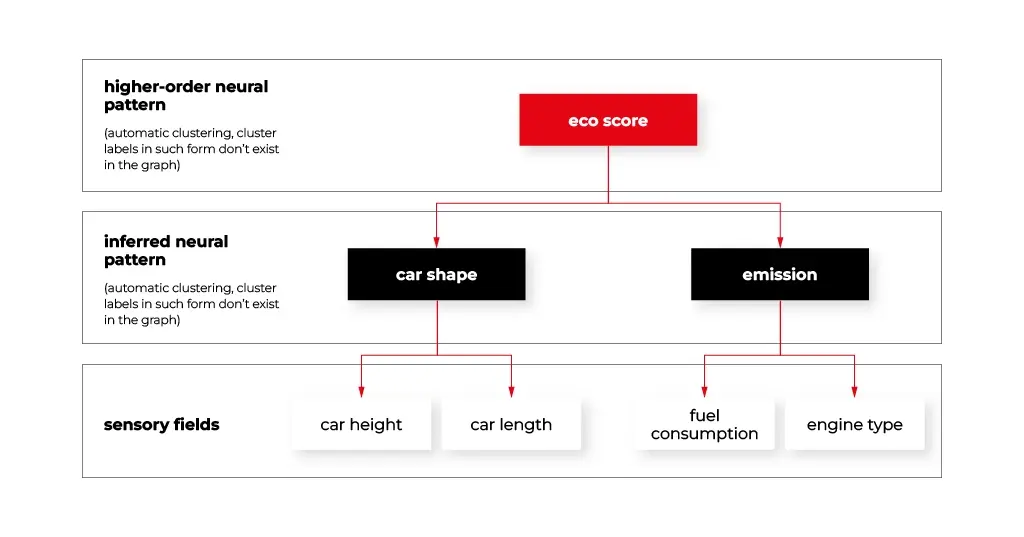
The information level can be managed by static (it does not change its internal structure) or dynamic (it may change its internal structure) associative graph data structures. A hybrid approach is also very useful here. For instance, CNN may be used as a feature extractor combined with associative graphs, as it happens in the human brain (assuming that CNN reflects the parietal cortex).  

The knowledge level may be represented by a set of dynamic or static graphs from the previous paragraph connected to each other with many various relationships creating an associative knowledge graph. 

The wisdom level is the most exotic. In the case of the associative approach, it may be represented by an associative system with various associative neural networks cooperating with other structures and algorithms to solve complex problems. 

Having that short introduction let’s dive deeper into the technical details of associative graphical approach elements. 

Sensory Field 

Many graph data structures can act as a sensory field. But we will focus on a special structure designed for that purpose. 

ASA-graph is a dedicated data structure for handling numbers and their derivatives associatively. Although it acts like a sensory field, it can replace conventional data structures like B-tree, RB-tree, AVL-tree, and WAVL-tree in practical applications such as database indexing since it is fast and memory-efficient.

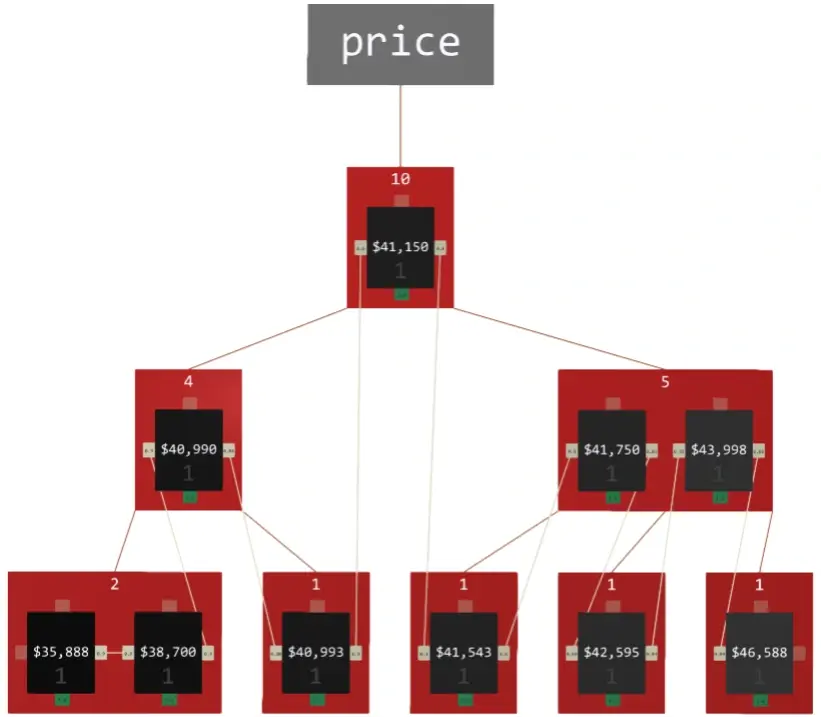
ASA-graphs are complex structures, especially in terms of algorithms. You can find a detailed explanation in this paper. From the associative perspective, the structure has several features which make it perfect for the following applications: 

• elements aggregation – keeps the graph small and devoted only to representing valuable relationships between data, 
• elements counting – is useful for calculating connection weights for some associative algorithms e.g., frequent patterns mining, 
• access to adjacent elements – the presence of dedicated, weighted connections to adjacent elements in the sensory field, which represents vertical relationship within the sensor, enables fuzzy search and fuzzy activation,  
• the search tree is constructed in an analogous way to DAG like B-tree, allowing fast data lookup. Its elements act like neurons (in biology, a sensory cell is often the outermost part of the neural system) independent from the search tree and become a part of the associative knowledge graph.

Efficient raw data representation in the associative knowledge graph is one of the most important requirements. Once data is loaded into sensory fields, no further data processing steps are needed. Moreover, ASA-graph automatically handles missing or unnormalized (e.g., a vector in a single cell) data. Symbolic or categorical data types like strings are equally possible as any numerical format. It suggests that one-hot encoding or other comparable techniques are not needed at all.  And since we can manipulate symbolic data, associative patterns mining can be performed without any pre-processing.

It may significantly reduce the effort required to adjust a dataset to a model, as is the case with many modern approaches. And all the algorithms may run in place without any additional effort. I will demonstrate associative algorithms in detail later in the series. For now, I can say that nearly every typical machine learning task, like classification, regression, pattern mining, sequence analysis, or clustering, is feasible.

Associative Knowledge Graph

In general, a knowledge graph is a type of database that stores the relationships between entities in a graph. The graph comprises nodes, which may represent entities, objects, traits, or patterns, and edges modeling the relationships between those nodes. 

There are many implementations of knowledge graphs available out there. In this article, I would like to bring your attention to the particular associative type inspired by excellent scientific papers which are under active development in our R&D department. This self-sufficient associative graph data structure connects various sensory fields with nodes representing the entities available in data.

Associative knowledge graphs are capable of representing complex, multi-relational data thanks to several types of relationships that may exist between the nodes. For example, an associative knowledge graph can represent the fact that two people live together, are in love, and have a joint loan, but only one person repays it. 

It is easy to introduce uncertainty and ambiguity to an associative knowledge graph. Every edge is weighted, and many kinds of connections help to reflect complex types of relations between entities. This feature is vital for the flexible representation of knowledge and allows the modeling of environments that are not well-defined or may be subject to change. 

If there weren’t specific types of relations and associative algorithms devoted to these structures, there wouldn’t be anything particularly fascinating about it. 

The following types of associations (connections) make this structure very versatile and smart, to some extent: 

• defining, 
• explanatory 
• sequential, 
• inhibitory, 
• similarity. 

The detailed explanation of these relationships is out of the scope of this article. However, I would like to give you one example of flexibility provided to the graph thanks to them. Imagine that some sensors are activated by data representing two electric cars. They have similar make, weight, and shape. Thus, the associative algorithm creates a new similarity connection between them with a weight computed from sensory field properties. Then, a piece of extra information arrives to the system that these two cars are owned by the same person.

So, the framework may decide to establish appropriate defining and explanatory connections between them. Soon it turns out that only one EV charger is available. By using dedicated associative algorithms, the graph may create special nodes representing the probability of being fully charged for each car depending on the time of day. The graph establishes inhibitory connections between the cars automatically to represent their competitive relationship. 

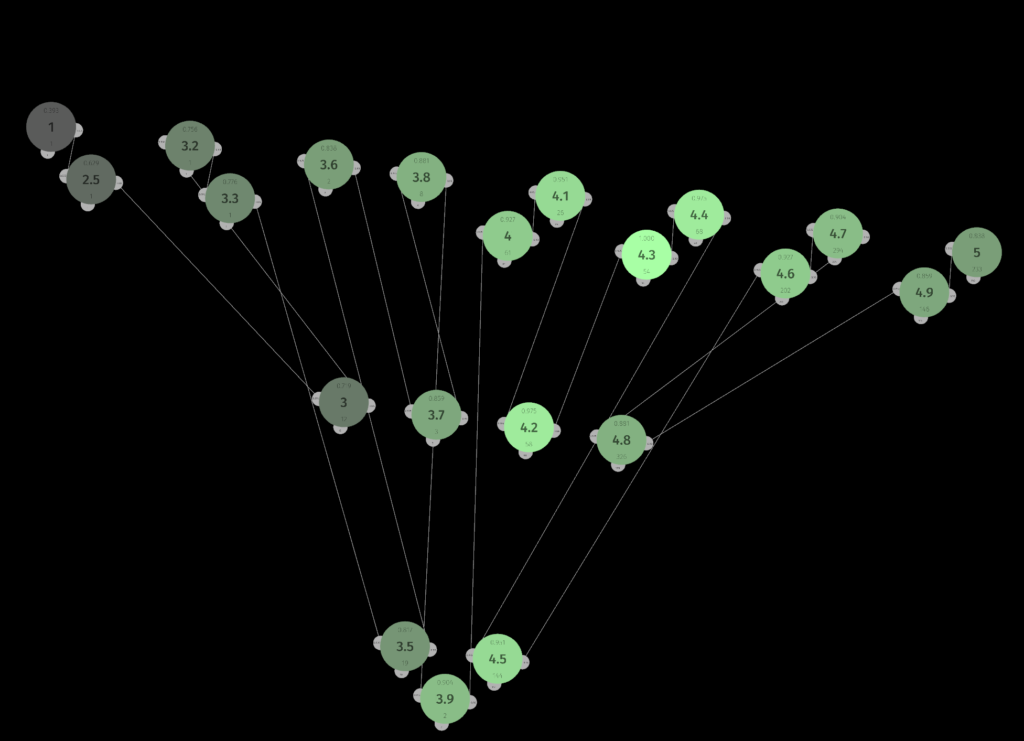
The image below visually represents the associative knowledge graph explained above, with the famous iris dataset loaded. Identifying the sensory fields and neurons should not be too difficult. Even such a simple dataset demonstrates that relationships may seem complex when visualized. The greatest strength of the associative approach is that relationships do not have to be computed – they are an integral part of the graph structure, ready to use at any time. The algorithm as a structure approach in action. 

A closer look at the sensor structure demonstrates the neural nature of raw data representation in the graph. Values are aggregated, sorted, counted, and connections between neighbors are weighted. Every sensor can be activated and propagate its signal to its neighbors or neurons. The final effect of such activation depends on the type of connection between them. 

What is important, associative knowledge graphs act as an efficient database engine. We conducted several experiments proving that for queries that contain complex join operations or such that heavily rely on indexes, the performance of the graph can be orders of magnitude faster than traditional RDBMS like PostgreSQL or MariaDB. This is not surprising because every sensor is a tree-like structure.

So, data lookup operations are as fast as for indexed columns in RDBMS. The impressive acceleration of various join operations can be explained very easily – we do not have to compute the relationships; we simply store them in the graph’s structure. Again, that is the power of the algorithm as a structure approach.

Associative Neural Networks 

Complex problems usually require complex solutions. The biological neuron is way more complicated than a typical neuron model used in modern deep learning. A nerve cell is a physical object which acts in time and space. In most cases, a computer model of neurons is in the form of an n-dimensional array that occupies the smallest possible space to be computed using streaming processors of modern GPGPU (general-purpose computing on graphics processing).

Space and time context is usually just ignored. In some cases, e.g., recurrent neural networks, time may be modeled as a discrete stage representing sequences. However, this does not reflect the continuous (or not, but that is another story) nature of the time in which nerve cells operate and how they work. 

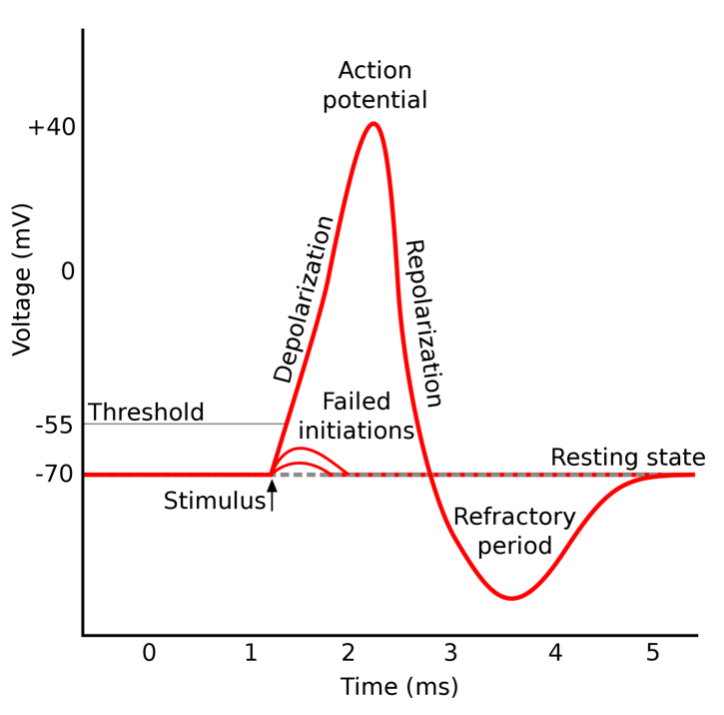
A spiking neuron is a type of neuron that produces brief, sharp electrical signals known as spikes, or action potentials, in response to stimuli. The action potential is a brief, all-or-none electrical signal that is usually propagated through a part of the network that is functionally or structurally separated, causing, for example, contraction of muscles forming a hand flexors group.

Artificial neural network aggregation and activation functions are usually simplified to accelerate computing and avoid time modeling, e.g., ReLu (rectified linear unit). Usually, there is no place for such things as refraction or action potential. To be honest, such approaches are good enough for most contemporary machine learning applications.  

The inspiration from biological systems encourages us to use spiking neurons in associative knowledge graphs. The resulting structure is more dynamic and flexible. Once sensors are activated, the signal is propagated through the graph. Each neuron behaves like a separate processor with its own internal state. The signal is lost if the propagated signal tries to influence a neuron in a refraction state.

Otherwise, it may increase the activation above a threshold and produce an action potential that spreads rapidly through the network embracing functionally or structurally connected parts of the graph. Neural activations are decreasing in time. This results in neural activations flowing through the graph until an equilibrium state is met. 

Associative Knowledge Graphs – Conclusions 

While reading this article, you have had a chance to discern associative knowledge graphs from a theoretical yet simplified perspective. The next article in a series will demonstrate how the associative approach can be applied to solve problems in the automotive industry. We have not discussed associative algorithms in detail yet. This will be done using examples as we work on solving practical problems.